Unit tests value proposition

June 1, 2016

The topic described in this article is part of my Unit Testing Pluralsight course.

I’m starting a new series which will be devoted to the topic of unit testing. In it, I’ll try to define what a valuable test is and show how the use of mocks fits into this picture. I’ll also describe the approach that I think has the best return of investments in terms of the value it provides.

Unit tests value proposition

There is an opinion that unit testing leads to a better design. I personally don’t think that unit testing in and of itself leads to anything.

It’s true that your unit test suite can become a good litmus test which tells you there’s something wrong with the code base. If the code is hard to unit test, then it probably requires improvement. However, the sole existence of a unit test suite doesn’t provide any guarantees. I’ve seen many code bases which were a mess despite a good test coverage.

In my opinion, the single most important benefit of unit testing is confidence. A good regression test suite enables you to refactor or add new features to your application without constant fear to break some existing functionality. I find this feeling liberating. Aside from the pure mental favor, such a test suite increases the speed of development and decreases the number of bugs. All these are invaluable benefits for any software development project.

Not all unit tests are made equal, however, and not all of them will automatically entail such gains. It’s important to differentiate various kinds of tests in terms of their value proposition.

So, what is a valuable unit test? It is a test which:

Has a high chance of catching a regression bug.
Has a low chance of producing a false positive.
Provides fast feedback.

High chance of catching a regression

The first point relates to the amount of code that gets exercised during a test. It is the number and, more importantly, the significance of the lines of code that are traversed during the test execution.

In that sense, trivial code is not worth to be tested because it’s short and doesn’t contain any business logic. Tests that cover trivial code just don’t provide a sensible chance of finding a regression. An example of such code is simple one line properties:

public class User
{
    public string Name { get; set; }
    public string Email { get; set; }
}

Low chance of producing a false positive

The second point is related to the way the test verifies the correctness of the system under test (SUT). The more the test is tied to the SUT’s implementation details, the more false positives it produces. A false positive is a situation where your test suite raises a false alarm: indicates an error, whereas, in the reality, everything works fine.

False positives can have a devastating effect on the health of your test suite. Just as non-determinism in tests, they dilute your ability to quickly spot the problem in case something goes wrong. Once you get accustomed to tests failing with every bit of refactoring, you stop paying attention to such failures, and legitimate failures get ignored with them.

The only way to reduce the chance of having false positives is decoupling your tests from the SUT’s implementation details as much as possible. Basically, you need to make sure you verify the end result your code generates, not the actual steps it takes to do that. Without such decoupling, you inevitably end up getting red tests in each refactoring, regardless of whether you break something or not.

Fast feedback

The final point is how quickly you get the feedback. It is important because the shorter your feedback loop, the faster you can adjust your course, and the less effort you waste going in a wrong direction. Quick feedback can only be provided by a fast test suite.

Unit tests value proposition: examples

These three attributes are mutually dependent. It’s impossible to maximize one of them without damaging the others. To illustrate this point, let’s consider end-to-end tests. They usually provide the best protection against regressions as they exercise all layers of your code base and thus have a high chance of catching a bug.

They are also mostly immune to false positives. A refactoring, if done right, doesn’t change the appearance of your system and thus doesn’t affect the end-to-end tests. The only thing such tests care of is how a feature behaves from the end user’s point of view, they don’t impose a concrete way to implement that feature.

The main drawback end-to-end tests possess is slowness. Any system that relies solely on such tests would have a hard time getting rapid feedback. And that is a deal-breaker for many development teams.

Similarly, it’s pretty easy to write a test that has a good chance of catching a regression but does it with a lot of false positives. An example here would be the following:

public class UserRepository
{
    public UserGetById(int id)
    {
        /* ... */
    }
 
    public string LastExecutedSqlStatement { get; private set; }
}

[Fact]
public void GetById_executes_correct_SQL_code()
{
    var repository = new UserRepository();
 
    User user = repository.GetById(5);
 
    Assert.Equal(
        "SELECT * FROM dbo.[User] WHERE UserID = 5",
        repository.LastExecutedSqlStatement);
}

As you can see, the test just copies the actual implementation of the GetById method in terms of the SQL code it generates.

Will this test catch a bug in case one sneaks through? Sure. A developer can mess up with SQL code generation and accidentally use ID instead of UserID, and the test will point that out.

Does this test have a low chance of producing a false positive? Absolutely not. Here are different variations of the SQL statement which lead to the same result:

SELECT * FROM dbo.[User] WHERE UserID = 5
SELECT * FROM dbo.User WHERE UserID = 5
SELECT UserID, Name, Email FROM dbo.[User] WHERE UserID = 5
SELECT * FROM dbo.[User] WHERE UserID = @UserID

The test will raise an error should you change the SQL script to any of them because it is tightly coupled to the repository’s implementation details. There are several ways the repository can do its job but the test insists on a particular one of them:

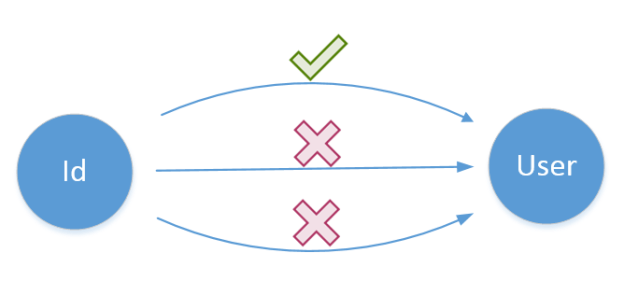
Testing an implementation detail

The fix is pretty simple here. We just need to shift our focus from hows of the SUT to its whats and verify the end result instead:

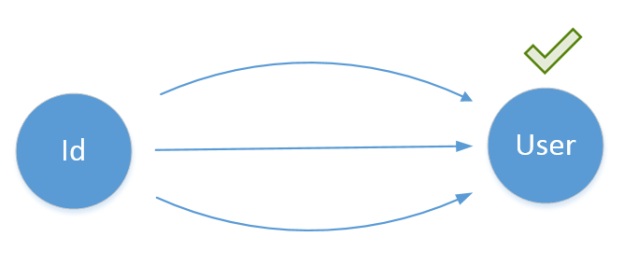
Testing the end result

In many cases, however, it’s hard to keep the balance between the three components. Anything less than end-to-end tests will be prone to refactoring to some degree. Also, you cannot achieve full confidence unless you exercise the majority of your code base which, in turn, is almost impossible to implement without knowing at least some implementation details of the SUT.

However, finding a good balance, despite being a hard task, is possible. In many cases, it requires architectural changes. What changes, you ask? That is something I’m going write about in the next post.

Summary

Let’s summarize the article with the following:

Unit tests in and of themselves don’t lead to a better design.
The main purpose of having a test suite is achieving confidence.
Not all tests are valuable. Valuable tests are tests that:
- Have a high chance of catching regressions,
- Have a low chance of producing false positives,
- Provide fast feedback.
You cannot maximize one of these attributes without damaging the others.