Hierarchy of value objects

December 24, 2018

This article is a response to a reader’s question. The question posed an interesting problem that I think will be interesting to a wider audience.

The problem introduction

I’ll start with the problem domain. There are two classes: Person and Document with the following business rules:

A person can have zero or one document.
A document can be assigned to only one person.
A document can’t exist without a person.

There are two types of documents in this domain model: IdentityCard and Passport. And here’s how the domain model looks on a diagram:

Domain model

As far as the underlying database goes, the first thought everyone (including me) would have is to introduce a table for the person class and another one for the documents. This second table would implement the table-per-hierarchy mapping strategy, where the whole class hierarchy is stored in a single table and individual elements are differentiated by a separate column called discriminator.

Here these tables are (the Type column is the discriminator):

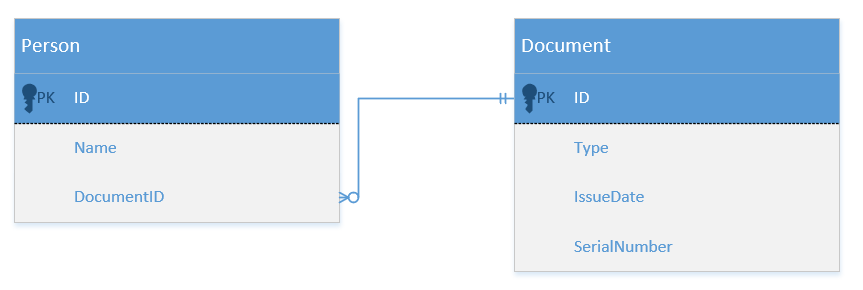
Database - initial

And here’s the domain model in code (public setters are for brevity):

public class Person : Entity
{
    public virtual string Name { get; set; }
    public virtual Document Document { get; set; }
}

public class Document : Entity
{
}

public class IdentityCard : Document
{
    public virtual DateTime IssueDate { get; set; }
}

public class Passport : Document
{
    public virtual string SerialNumber { get; set; }
}

The ubiquitous virtual keywords is due to the use of NHibernate.

The solution looks good but the problem with this implementation is that if you try to assign a person a new document, the old document would still remain in the database, it won’t be deleted automatically. So, something like this:

var person = new Person { Name = "Name" };
person.Document = new IdentityCard(DateTime.Now);
Flush(); // both the person and the document are created

person.Document = new Passport("Serial Number");
Flush(); // the new document is assigned but the old one remains in the database

would lead to having two documents in the database. Only one of them will be referenced by a person, the other one would become orphaned. You’ll have to delete the second document manually using a repository or by calling the NHibernate session directly.

Toying with NHibernate cascade options

How to fix this?

NHibernate exhibits rich cascading capabilities. You can use them to inform NHibernate what to do with the child entities when you create, update, or delete the parent one. Here are the most popular cascade options:

None does nothing.
Save-update creates or updates the child entity when you create or update the parent one.
All -- the same as save-update plus deletion. Meaning that if you delete the parent entity, the child one gets deleted with it.
All-delete-orphans -- the same as all plus deletion of orphaned entities.

The all-delete-orphans option is useful with collections of child entities. For example, should the Person class had a list of documents, with all, the documents will only get deleted when the person itself is deleted. Whereas with all-delete-orphans, you can delete a document by merely removing it from the person’s document collection. No need to delete the person.

The last option looks like a perfect match for our problem but here’s the thing. It only works with one-to-many relationships. Should Person had a collection of documents, that would be it — just modify the mapping file and be done with it. But in our case, a person can have only one document, and that is a many-to-one (or one-to-one) relationship, not one-to-many.

Hierarchy of value objects

So, what to do?

Before proceeding to the solution, let’s look at the domain model again. What is Document here, an entity or a value object? The main factor that differs an entity from a value object is the necessity to keep track of it. If you need to know what happened to a particular object in your domain model and differentiate this object from others even after you modify it, that’s an entity. If you are fine with replacing one with another, that’s a value object.

In our domain model, a document can only be assigned to a single person. Also, a document can’t existing on its own. This is a strong indicator that Document is a value object. You don’t care what happens with the old document when you replace it with a new one. Moreover, you want to get rid of the old one so that it doesn’t litter the database. That’s the attributes of a value object right there.

And by the way, it’s a good example of a value object. It’s good particularly because it shows that a concept isn’t inherently an entity or a value object. Its treatment depends on the requirements of a particular application/bounded context. In another bounded context Document could very well be an entity, just not in this one.

As I wrote in my article Entity vs Value Object: the ultimate list of differences, the best way to store value objects in the database is to include them into the parent’s table. And that’s what we need to do here as well.

Merging Document's data with Person is a natural solution that allows you to make Document follow the value object semantics. Just like you can replace the name of a Person with any other name you want and don’t need to worry about deleting the old name from the database, you will also be able to easily replace the Person's document with a new one and forget about all the headaches of the existing implementation.

Remember: separate tables are for entities. Should Document be an entity, we wouldn’t want to get rid of its instance when replacing it with a new one. In this case, the existing implementation would be the best fit. However, value objects are best kept inside their entities. You wouldn’t introduce a new table for the person’s name, would you? Neither should you introduce it for the document.

Alright, so we need to move all the data from the Document table to the Person one. This is what it would look like:

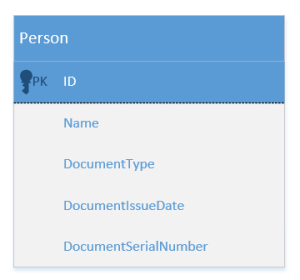
Database final

There’s one problem, though: the hierarchy of documents. How can you map that hierarchy to the database, given that there’s no separate table for documents anymore? The built-in ORM inheritance functionality only works for entities. More specifically, this functionality requires a separate table or several separate tables.

We’ll need a custom inheritance implementation here — a wrapper class that would encompass the hierarchy of documents. We’ll use this wrapper in place of a document in Person, like this:

public class DocumentContainer
{
    private DocumentType _type;
    private DateTime? _issueDate;
    private string _serialNumber;

    public Document Document
    {
        get
        {
            switch (_type)
            {
                case DocumentType.IdentityCard:
                    return new IdentityCard(_issueDate.Value);

                case DocumentType.Passport:
                    return new Passport(_serialNumber);

                default:
                    throw new ArgumentOutOfRangeException();
            }
        }
        set
        {
            switch (value)
            {
                case IdentityCard identityCard:
                    _issueDate = identityCard.IssueDate;
                    _serialNumber = null;
                    _type = DocumentType.IdentityCard;
                    break;

                case Passport passport:
                    _issueDate = null;
                    _serialNumber = passport.SerialNumber;
                    _type = DocumentType.Passport;
                    break;
            }
        }
    }
}

public class Person : Entity
{
    public virtual string Name { get; set; }

    private readonly DocumentContainer _document;
    public virtual Document Document
    {
        get => _document.Document;
        set => _document.Document = value;
    }
}

So basically what I did here is I re-implemented the table-per-class-hierarchy mapping available in ORMs out of the box. It’s just I did that not for entities but for value objects whose data is part of the parent entity’s table. The wrapper contains all the fields from all the classes in the hierarchy and updates or nullifies them depending on the type of the value object.

This manual mapping seems clunky but the good part is that it’s hidden from the clients of the Person class. What Person exposes is the nice and clean Document instance — just as before. But this time it’s a proper value object — without an identity, and with the lifetime which is fully controlled by the parent entity.

Here’s the full source code, including the NHibernate mapping: https://gist.github.com/vkhorikov/61f873671630db5a4e0234f9912c660e

This technique is similar to what I wrote about a couple years back: Nesting a Value Object inside an Entity. In this article, I too recommended to introduce a wrapper on top of a value object and hide that wrapper away from the eyes from the class’s clients.

This is by the way a re-occurring topic I encounter in a lot of complex scenarios. If you can’t figure out how to map something using plain ORM, create a wrapper and map that wrapper instead. Just make sure you don’t expose it with the class’s public API.

Summary

NHibernate doesn’t support the all-delete-orphans cascade feature in many-to-one or one-to-one relationships. Only one-to-many relationships are eligible.
The best way to store value objects in the database is by in-lining them into the parent entity’s table, even if it’s not just a single value objects but a hierarchy of them.
To implement a hierarchy of value objects, create a wrapper class with all data fields from all the value objects in the hierarchy. Map that class as a regular value object.
Don’t expose the wrapper to the class’s clients.