Growing Object-Oriented Software, Guided by Tests Without Mocks

Let me first explain why I’m doing a review of this book. If you read this blog regularly, you probably noticed that I’m pretty much against using mocks in tests. Because of that, I sometimes receive feedback which states that the code I’m taking as an example just doesn’t employ mocking correctly and thus my arguments are not quite valid.

So here I’ll take the most canonical example of using mocks I could find - the one from the GOOS book - and will show how the use of mocks damages the design. I’ll also show how much simpler the code base becomes when you get rid of mocks and apply the guidelines I described in the previous posts of this series.

The second reason for this review is to point out which advice in the book I consider good and which not. There are plenty of great tips and guidelines in the book, and there is also advice that can harm your application should you implement it in practice.

Alright, I’ll start with the good parts, most of which reside in the first two sections of the book.

The authors put a great emphasis on the tests being a safety net which helps reveal regression errors. This is indeed an important role of them. In fact, I think it’s the most important one. It provides confidence which, in turn, enables fast movement towards the business goals. It’s hard to overestimate how much more productive you become when you are sure that the feature or refactoring you just implemented doesn’t break the existing functionality. This feeling is liberating.

The book also describes the importance of setting up the deployment environment in early stages. That should be your first priority when starting a green field project as it allows you to reveal potential integration issues right away, before you write a substantial amount of code.

To do that, the authors propose building a "walking skeleton" - the simplest version of your application possible which at the same time crosses all layers end-to-end. For example, if it’s a web application, the skeleton can show a simple HTML page which renders some string from the real database. This skeleton should be covered with an end-to-end test which should become the first test in your test suite.

This technique allows you to focus on building a deployment pipeline without paying too much attention to the application’s architecture. The faster you get feedback, the better.

The book proposes a two-level TDD cycle:

That is starting each feature with an end-to-end test and building your way to passing it with the regular red-green-refactor cycle.

End-to-end tests here act more as a progress measurement and some of them may fail because the features they cover are still in development. Unit tests, at the same time, is a regression suite and should pass at all times.

It’s important that end-to-end tests touch as many external systems as possible. It would help you reveal integration issues. At the same time, the authors admit that you’ll often have to fake some external systems anyway. It is an open question what to include into end-to-end tests; you need to make a decision in each case separately. For example, if you work with an external banking system, it’s not practical to create real money transactions every time you want to test integration with it.

The book proposes to extend the classic 3-step TDD cycle with an additional step: clearing up the diagnostics message.

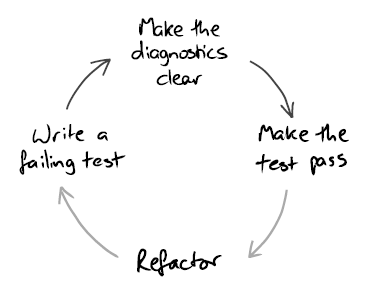
This practice helps make sure that when the test fails, you will be able to understand what’s wrong with your code just by looking at the failure message and won’t have to launch the debugger.

The authors advice to develop the application end to end starting from the beginning. Don’t spend too much time on polishing your architecture, start with some input that comes from the outside world (for example, from the UI) and process that input entirely, down to the database level with the minimum amount of code possible. In other words, work with vertical slices of functionality, don’t build the architecture up-front.

Another great advice is to unit-test behavior, not methods. They are often not the same thing as a single unit of behavior may cross multiple methods at once. This practice will help you build tests that answer the "what" question instead of "how".

Another interesting point is context-independence of the SUT:

That is basically the concept of domain model isolation. The domain classes shouldn’t know or depend on any external system. You should be able to extract it out of the context in which it runs without additional effort. Aside from the ability to easily test the code base, such technique greatly simplifies it as you are able to focus on your domain model without paying attention to concerns not related to your domain.

The book proposes the somewhat famous rule "Only mock types that you own". That is, you should use test doubles to substitute only the types you created yourself. Otherwise, you are not guaranteed to mimic their behavior correctly. The guideline basically boils down to writing your own gateways for each external service you use.

It’s interesting that the authors break this rule for a couple of times throughout the book. The external types in those cases are quite simple, though, so there’s not much point in substituting them with own implementations.

By the way, Gojko Adzic in his talk Test automation without a headache refines this rule to "Only mock types that you understand". And I think this version better fits the intention behind the guideline. If you fully understand how the type works, it doesn’t matter who its author is, you are able to fully simulate its behavior with a mock and thus don’t need any additional wrappers on top of it.

Despite all the great tips and techniques the book proposes, the amount of potentially harmful advice is quite substantial as well.

The book is a strong proponent of the collaboration verification style of unit testing even when it comes to communication between individual objects inside the domain model. In my opinion, it’s the main shortcoming of the book. All other shortcomings flow from this one.

To justify this approach, the authors allude to the definition of Object-Oriented Design given by Alan Kay:

They then conclude that interactions between objects is what you should focus on foremost in unit tests. By this logic, the communication pattern between classes is what essentially comprises the system and identifies its behavior.

There are two problems with this viewpoint. First, I wouldn’t bring the Alan Key’s definition of OOD here. It’s quite vague to build such a strong argument upon and has little to do with how modern strongly-typed OOP languages look like today.

Here’s another famous quote of him:

And of course, you can safely substitute C++ with C# or Java here.

The second problem with this line of thinking is that separate classes are too fine-grained to treat them as independent communication agents. The communication pattern between them tend to change often and has little correlation with the end result we should aim at verifying.

As I mentioned in the previous post, the way classes inside the domain model talk to each other is an implementation detail. The communication pattern only becomes part of API when it crosses the boundary of the system: when your domain model starts interacting with external services. Unfortunately, the book doesn’t make this distinction.

The drawbacks of the approach the book proposes become vivid when you consider the sample project it goes through in the 3rd part. Not only focusing on collaboration between classes entails fragile unit tests that couple to the SUT’s implementation details, but it also leads to an overcomplicated design with circular dependencies, header interfaces, and an excessive number of layers of indirection.

In the rest of this article, I’m going to show you how the book’s implementation can be modified and what effect that modification has on the unit test suite.

The original code base is written in Java, the modified version is in C#. Note that it is a full rewrite, not just a partial one. I took the problem from the book and implemented it from scratch up to the point where the book left it off. It means that along with the domain model and the unit tests, there also are end-to-end tests which work with UI and an external XMPP server. The UI is written in WPF; as for the XMPP server, I wrote a simple emulator using named pipes.

Before diving into the code base, let me introduce the problem domain first. The sample application is Auction Sniper - a robot aimed at participating in online auctions. Here’s its UI interface:

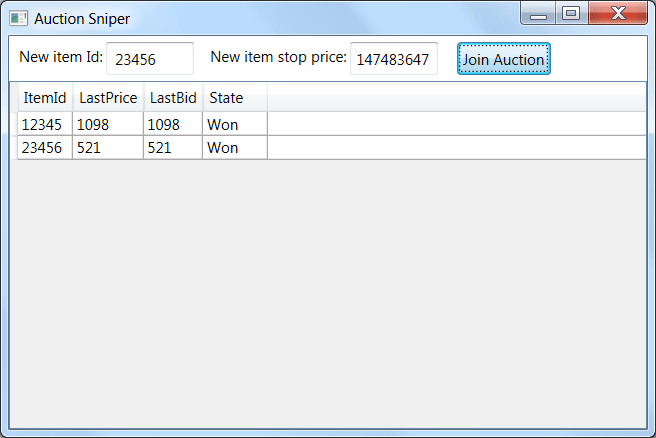
Item Id is the identifier of an item that is being sold; Stop Price is the maximum price you as a user are willing to pay for this item; Last Price is the latest bid amount came from the auction server; Last Bid is the latest bid Auction Sniper made on your behalf; State is the state of the auction. In the example above, you can see the application won both of the items, that’s why the last prices equal to the last bids - both came from our software.

Each row in the grid here represents a separate agent which listens to the events coming from the auction server and responds to them accordingly. The business rules can be summarized with the following picture:

Each agent (they are also called Auction Snipers) starts from the top of the picture, in the Joining state. It then waits for the server to send an event about the current state of the auction - what the last price was, from what user, and what the minimum increment should be in order to outbid the last price. This event is named Price event.

If the bid required is less than the stop price we as a user set up for this item, the application sends a bid and transitions to the Bidding state. If a new price event shows that our bid is leading, Sniper does nothing and moves to the winning state. Finally, the second event the auction server can send is the Close event. When it comes, the application is looking at what state it is currently in for the given item. The Winning state goes to Won, and all others go to Lost.

So basically what we have here is an automatic auction participant that sends commands to the server and maintains an internal state machine.

Let’s now look at the architecture the book came up with. Here’s the diagram (click to enlarge):

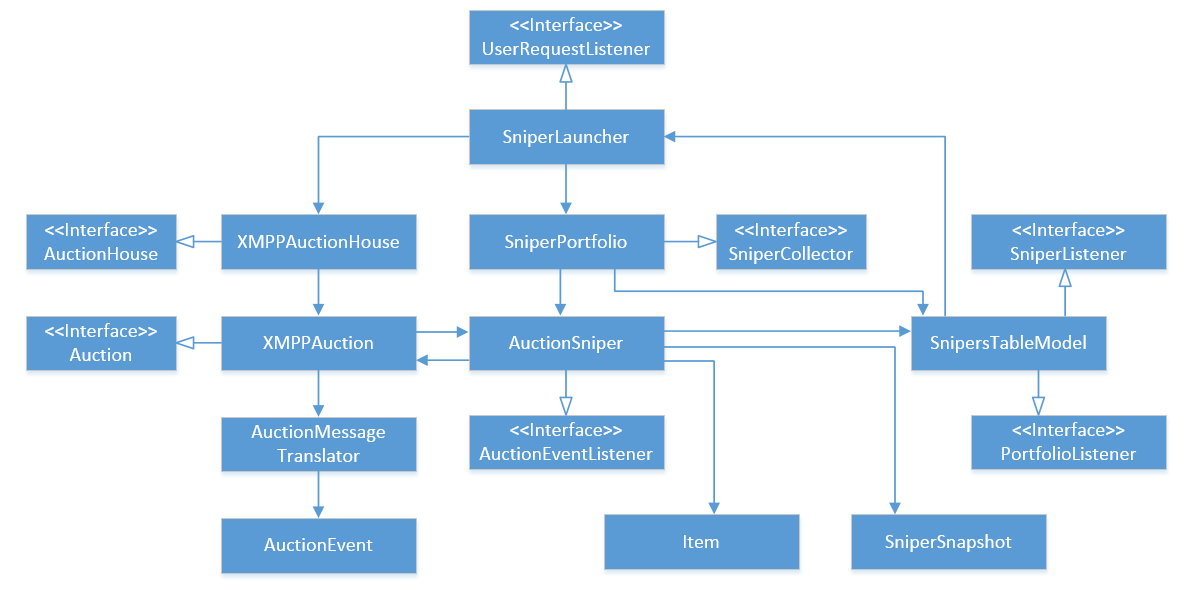
If you think it is too complicated for such a task at hand, that’s because it is. So, what issues do you see here?

The very first thing that meets the eye is lots of header interfaces. That are interfaces that fully mimic a single class that implements them. For example, the XMPPAuction class has a 1-to-1 correspondence to the Auction interface, AcutionSniper - to AuctionEventListener, and so on. Interfaces with the only implementation don’t represent an abstraction and generally considered a design smell.

Below is the same diagram without interfaces. I removed them so you have less visual clutter:

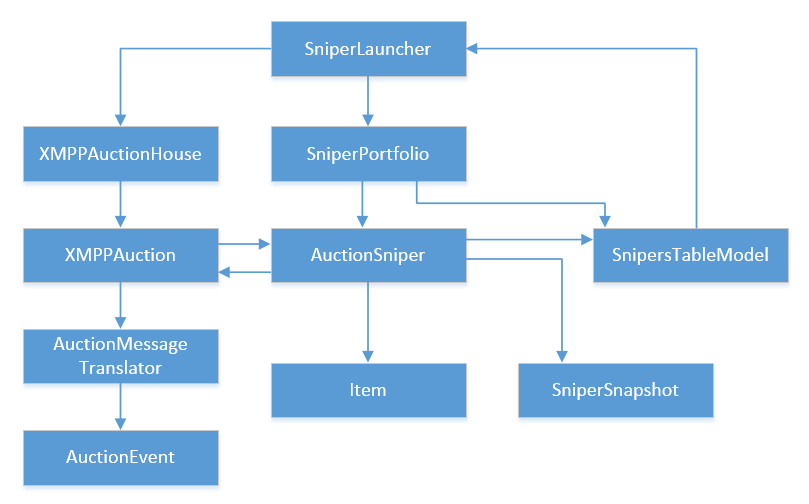
The second issue here is cyclic dependencies. The most obvious one is between XMPPAuction and AuctionSniper, but there are several others as well. For example, AuctionSniper refers to SnipersTableModel which refers to SniperLauncher, and so on until the connection comes back to AuctionSniper.

Cyclic dependencies add tremendous cognitive load when you try to read and understand the code. The reason here is that, with such dependencies, you don’t know where to start from. In order to understand what one of the classes does, you need to push the whole graph of its siblings into your head.

Even after I rewrote the original implementation, I often had to refer to the diagram to understand how different classes and interfaces relate to each other. We as humans are good at processing hierarchies, not graphs. Scott Wlaschin has a great article that dives into the details of this subject: Cyclic dependencies are evil.

The third problem is lack of the domain model isolation. Here’s how the architecture looks like from a DDD perspective:

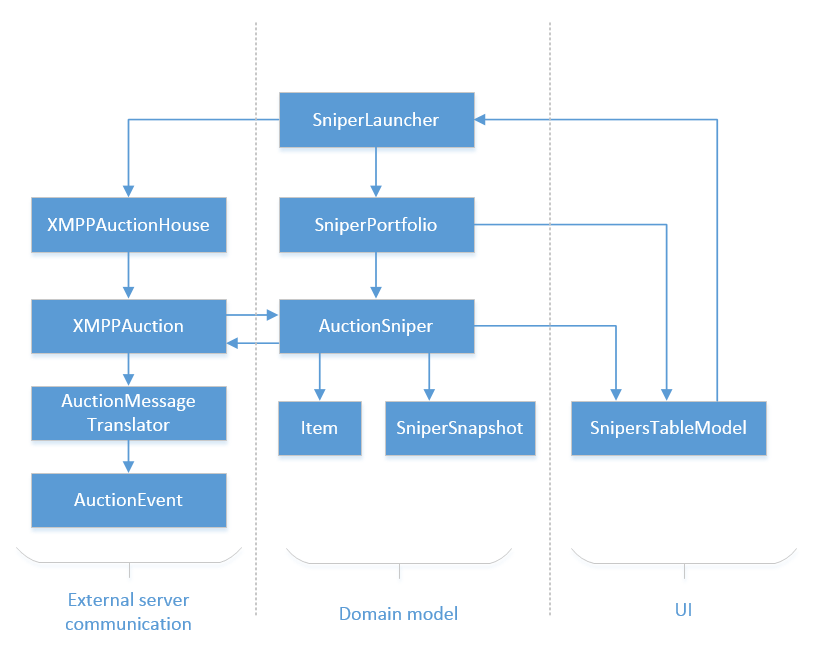
The classes in the middle of it comprise the domain model. At the same time, they communicate with the Auction server (on the left) on one hand, and with the UI (on the right) on the other. For example, SniperLauncher talks to XMPPAuctionHouse, and AuctionSniper - to XMPPAcution and SnipersTableModel.

Of course, they do it by using interfaces, not the actual classes but again, introducing a header interface for something doesn’t mean you automatically start adhering to the Dependency Inversion principle. It’s just a hack to avoid reaching genuine domain model isolation.

Ideally, the domain model should be self-contained, classes inside of it shouldn’t talk to classes from the outside world, not using concrete implementations, nor their interfaces. Proper isolation would mean the domain model can be tested in a functional manner without involving mocks.

These shortcomings is what you often end up with when you focus on testing collaborations between classes, and not their public API. Such attitude leads to creating header interfaces because otherwise, it’s impossible to mock those classes out. Also, you have lots of circular dependencies and you have domain entities communicating directly to the outside world.

Let’s now look at the unit tests themselves. Here’s one:

Putting away its collaboration nature which means that we need to create and support a substantial amount of mock machinery just to verify the communication pattern, here we have implementation details leaking into the test. The when statement means that the test becomes aware of the internal SUT’s state and mimics that state in order to perform the verification.

Here’s another example:

This sample is a clear example of implementation details leakage. Here, the test implements a fully-fledged state machine in order to verify that the methods are invoked in this particular order:

Because of the coupling to the SUT’s internals, tests like this one are extremely fragile. Any non-trivial refactoring will make them fail regardless of whether that refactoring broke something or not. It significantly diminishes their value. Such tests result in lots of false positives and because of that cannot act as a reliable safety net. Here you can read more on what I consider a valuable unit test suite: Unit tests value proposition.

The full source code for the book’s sample project can be found here.

Alright, it’s a lot of strong statements so far. Clearly, I need to provide an alternative solution in order to back up my words with some real code. You can find the full source code of that solution on GitHub. I’ll now describe its architecture and the reasoning behind it.

To understand how the project can be implemented with a proper domain model isolation, without circular dependencies and without excessive number of needless abstractions, let’s consider what responsibilities AuctionSniper has. It receives events from the server and responds back with some commands, maintaining an internal state machine along the way:

And that’s basically it. In fact, it’s almost ideal functional architecture and there’s nothing preventing us from implementing it as such.

Here’s the class diagram for the alternative architecture:

Several points to note here. First of all, the domain model is fully isolated from the outside world. The classes in it don’t talk to the view model or the XMPP Server, all references point *to* the domain classes, not the other way around.

All communication with the outside world, be it the auction server or UI, is handled by the Application Services layer which in our case is AuctionSniperViewModel. It acts as a shield that protects the domain model from the unwanted influence. It filters the incoming requests and interprets the outcoming responses.

Secondly, the domain model doesn’t contain any cyclic dependencies. The class structure is a tree which means that a potential reader of this code has a clear place to start learning it from. He can proceed from the leafs of the tree up to its roots step by step, without having to push the whole diagram into his head. This code base is pretty simple of course, and I’m sure you wouldn’t have any troubles reading it even in the face of circular dependencies. In more complex projects, however, a clear tree-like class structure gives a great benefit in terms of simplicity.

By the way, the famous DDD pattern - Aggregate - is aimed at solving this exact problem. By having multiple entities grouped into a single aggregate, we reduce the number of connections in the domain model and thus make the code base simpler.

The third point to note here is that the code base above doesn’t have any interfaces. Not a single one. This is one of the benefits of having a fully isolated domain model: you just don’t need to introduce interfaces unless they represent a real abstraction. Here, we don’t have any.

Note that with this architecture, we adhere to the guideline I described in the Pragmatic unit testing article. Classes in it either contain business knowledge (the classes inside the domain model) or communicate to the outside world (the application services layer), but never both. With such separation of concerns, we are able to focus on one thing at a time: we either think about the domain logic or decide how to respond to the stimulus from the UI and the auction server.

Again, this leads to greater simplicity and, therefore, better maintainability. Here’s how the most important part of the Application Services layer looks like:

We get a string from the auction server, transform it to an event (the validation is baked into this step), feed it to the auction sniper and if the resulting command is not None, send it back to the auction server. As you can see, the lack of business logic makes the Application Services layer trivial.

The idea with the dump Application Services layer is very similar to the idea with dump Mutable Shell which I described in my immutable architecture post.

Another benefit of having an isolated domain model is the ability to test it using the functional style of unit testing. We can treat each piece of behavior in isolation and verify the end result it produces, without paying attention to how that end result is achieved. And in doing so, we are able to operate the existing domain concepts making the tests extremely readable.

For example, this test checks how Sniper that just joined to an action behaves after getting a Close event:

It verifies that the command the sniper responds with is empty, meaning that the sniper doesn’t take any action, and the state of the sniper is Lost after that.

Here’s another example:

This one makes sure the sniper bids when the current price of the lot and the minimum increment is lower than the stop price.

The only place where mocks would potentially be justified is when testing the Application Services layer which communicates with the external systems. But as this part is covered by end-to-end tests, it is not needed. By the way, the end-to-end tests in the book are great, I haven’t found anything to improve or change in them.

Not only does focusing on the communication pattern between individual classes lead to fragile unit tests, it also entails architectural damage (one could call it test-induced design damage).

To avoid that damage, make sure you:

This post might seem a bit harsh but no offense is intended. Despite all said above, the book has lots of extremely valuable material. It’s just you need to carefully separate it from the other parts.

If you enjoyed this article, be sure to check out my Pragmatic Unit Testing Pluralsight course where I show the full process of refactoring the original architecture from the book.

I recommend you to take a closer look at the alternative implementation. It’s actually quite simple. When working on it, I spent most of the time writing an emulator for the XMPP client and server (which you don’t need to look at anyway), the other parts are simple and straightforward.