DRY vs DAMP in Unit Tests

June 8, 2020

In this post, we’ll make a deep dive into the DRY and DAMP principles and will talk about the false dichotomy around them.

The DRY and DAMP principles

The DRY principle stands for "Don’t Repeat Yourself" and requires that any piece of domain knowledge has a single representation in your code base. In other words, in requires that you don’t duplicate the domain knowledge.

The DAMP principle stands for "Descriptive and Meaningful Phrases" and promotes the readability of the code.

DRY vs. DAMP: the dichotomy

You can often hear that people put these two principles in opposition to each other. DRY and DAMP are usually represented as two ends of the spectrum that covers all of your code:

DRY and DAMP as two ends of the spectrum

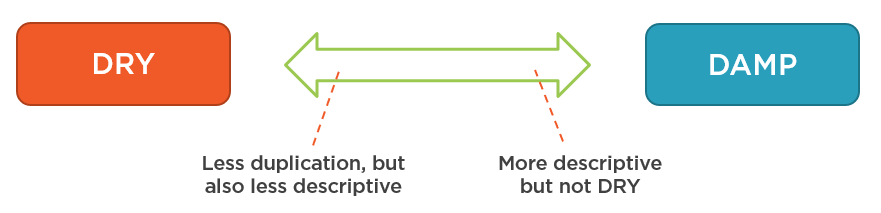
You can choose to make your code more descriptive at the expense of the DRY principle (and thus lean towards the DAMP end of the spectrum) or you can choose to remove duplication, but at the cost of the code becoming less expressive. In other words, you can’t adhere to both principles with the same piece of code.

You may also hear the guideline saying that:

For your production code, you should err on the side of the DRY principle
For the test code, you should favor DAMP over DRY

I strongly disagree with this opposition.

But let’s first take an example, to understand where this guideline comes from. I’ll then describe why this guideline misses the point.

Let’s say we have a UserController with two methods:

public class UserController
{
    public string Register(string userName, string email)
    {
        User userByName = _dbContext.Users
            .SingleOrDefault(x => x.UserName == userName);
        if (userByName != null)
            return "User with such username already exists";

        User userByEmail = _dbContext.Users
            .SingleOrDefault(x => x.Email == email);
        if (userByEmail != null)
            return "User with such email already exists";

        // Register the user

        return "OK";
    }

    public string EditPersonalInfo(string userName, string email)
    {
        User currentUser = GetCurrentUser();

        User userByName = _dbContext.Users
            .SingleOrDefault(x => x.UserName == userName && x.UserName != currentUser.UserName);
        if (userByName != null)
            return "User with such username already exists";

        User userByEmail = _dbContext.Users
            .SingleOrDefault(x => x.Email == email && x.Email != currentUser.Email);
        if (userByEmail != null)
            return "User with such email already exists";

        // Update personal info

        return "OK";
    }
}

Both of the methods check for user name and email uniqueness before making the changes. These checks aren’t exactly the same (EditPersonalInfo takes into account the current user’s name and email), but close enough to be worth extracting into one place.

Here’s how we can do that:

public class UserController
{
    public string Register(string userName, string email)
    {
        if (UserNameAlreadyExists(userName, null))
            return "User with such username already exists";

        if (UserEmailAlreadyExists(email, null))
            return "User with such email already exists";

        // Register the user

        return "OK";
    }

    public string EditPersonalInfo(string userName, string email)
    {
        User currentUser = GetCurrentUser();

        if (UserNameAlreadyExists(userName, currentUser.UserName))
            return "User with such username already exists";

        if (UserEmailAlreadyExists(email, currentUser.Email))
            return "User with such email already exists";

        // Update personal info

        return "OK";
    }

    private bool UserNameAlreadyExists(string name, string currentUserName)
    {
        IQueryable<User> query = _dbContext.Users
            .Where(x => x.UserName == name);

        if (currentUserName != null)
        {
            query = query.Where(x => x.UserName != currentUserName);
        }

        User user = query.SingleOrDefault();

        return user != null;
    }

    private bool UserEmailAlreadyExists(string email, string currentUserEmail)
    {
        /* Same for email */
    }
}

This version is much cleaner. It also adheres to the DRY principle — the common bits get reused across the two methods. (Notice that I moved the checks for uniqueness to private methods, but they could also be repository methods, depending on your project’s specifics.)

So, that’s the example of the first part of the guideline — favoring DRY in the production code. The benefits are pretty self-evident: the code in the two controller methods gets simpler and, more importantly, the knowledge of how to do the uniqueness checks now resides in one place.

Let’s now look at the second part of the guideline — preferring DAMP in the test code. Let’s say we’ve got a CalculatorController and two tests that check its functionality:

[Fact]
public void Division_by_zero()
{
    // Arrange
    int dividend = 10;
    int divisor = 0;
    var calculator = new CalculatorController();

    // Act
    Envelope<int> response = calculator.Divide(dividend, divisor);

    // Assert
    response.IsError.Should().BeTrue();
    response.ErrorCode.Should().Be("division.by.zero");
}

[Fact]
public void Division_of_two_numbers()
{
    // Arrange
    int dividend = 10;
    int divisor = 2;
    var calculator = new CalculatorController();

    // Act
    Envelope<int> response = calculator.Divide(dividend, divisor);

    // Assert
    response.IsError.Should().BeFalse();
    response.Result.Should().Be(5);
}

These tests also have common bits, that could be extracted like this:

/* The initialization code that is common for both tests */
int _dividend = 10;
CalculatorController _calculator = new CalculatorController();

[Fact]
public void Division_by_zero()
{
    // Arrange
    int divisor = 0;

    // Act
    Envelope<int> response = _calculator.Divide(_dividend, divisor);

    // Assert
    response.IsError.Should().BeTrue();
    response.ErrorCode.Should().Be("division.by.zero");
}

[Fact]
public void Division_of_two_values()
{
    // Arrange
    int divisor = 2;

    // Act
    Envelope<int> response = _calculator.Divide(_dividend, divisor);

    // Assert
    response.IsError.Should().BeFalse();
    response.Result.Should().Be(5);
}

This time the refactoring doesn’t feel as good as in the previous example, does it?

Indeed, such a refactoring is an anti-pattern:

It introduces high coupling between tests — If you need to modify the calculator setup in one test, it will affect the other test too.

Such coupling becomes hard to trace really quickly. Changes in one test may ripple through the remaining tests and may introduce unexpected bugs in them.

Try to always follow this rule of thumb: a modification of one test should not affect other tests. For that, you need to avoid sharing state between tests. The two private fields (_dividend and _calculator) are an example of such a shared state.
It diminishes test readability — After extracting the two lines, you no longer see the full picture just by looking at individual tests. You have to examine the whole class in order to understand what the test does.

Even if there’s not much of arrangement logic, for example, only instantiation of the calculator, like in the example above, you are still better off moving that logic directly to the test method. Otherwise, you’ll wonder if it’s really just instantiation or maybe there’s something else is being configured here as well. A self-contained test doesn’t leave you with such uncertainties.

That’s where the guideline of preferring DAMP over DRY in tests comes from. The initial version of the two tests is better — it’s more expressive, even if at the expense of code repetition.

The DRY vs. DAMP dichotomy is false

So, again, the common belief is that you can’t adhere to both DRY and DAMP with the same piece of code, and the choice should be the following:

For the production code, prefer DRY over DAMP
For the test code, do the opposite choice.

This dichotomy between DRY and DAMP is false. Both principles are equally important in both the production and test code. In fact, you don’t have to make a trade-off between these two principles at all.

To see why, we need to step back and make a closer look at the DRY principle. As I mentioned earlier, it stands for "Don’t Repeat Yourself" and requires that any piece of domain knowledge has a single representation in your code base. The words domain knowledge are key here. DRY is not about duplicating code. It is specifically about duplicating domain knowledge.

The following method is a nice way to visualize this distinction:

public static string GetStatus(bool isLocked)
{
    return (isLocked ? "L" : "Unl") + "ocked";
}

This code is what you get when you try to apply the DRY principle not to the domain knowledge but to the code itself.

Of course, this method is ridiculous — it tries to squeeze together as many characters as possible. It should have listed these two words separately, like this:

public static string GetStatus(bool isLocked)
{
    return isLocked ? "Locked" : "Unlocked";
}

The fact that these two words have some common piece in them doesn’t mean they share domain knowledge. The common piece is just a coincidence, there’s nothing that inherently unites them.

The words represent two separate pieces of domain knowledge. Particularly, the knowledge of how the Locked and Unlocked statuses are displayed to the user. You should be able to change one of these words without affecting the other. For that, you need to decouple them by splitting into two separate strings.

This is essentially the same misapplication of the DRY principle as in previous example (I’m copying it here for convenience):

/* The initialization code that is common for both tests */
int _dividend = 10;
CalculatorController _calculator = new CalculatorController();

[Fact]
public void Division_by_zero()
{
    // Arrange
    int divisor = 0;

    // Act
    Envelope<int> response = _calculator.Divide(_dividend, divisor);

    // Assert
    response.IsError.Should().BeTrue();
    response.ErrorCode.Should().Be("division.by.zero");
}

[Fact]
public void Division_of_two_values()
{
    // Arrange
    int divisor = 2;

    // Act
    Envelope<int> response = _calculator.Divide(_dividend, divisor);

    // Assert
    response.IsError.Should().BeFalse();
    response.Result.Should().Be(5);
}

Here, we are also applying the DRY principle not to the domain knowledge, but to the code itself, which is incorrect. The two shared lines at the top don’t represent any domain knowledge, they are just happen to be the same for both tests. Therefore, they should not be reused.

DRY and DAMP as How-to’s and What-to’s

I hope you can see now why the dichotomy between DRY and DAMP is false. You should avoid the code reuse shown in the previous example, but not because DRY somehow doesn’t apply to tests. It’s because such a reuse is an misapplication of DRY, and it is a misapplication regardless of whether you do that in tests or in the production code.

Alright, so the DRY principle should only be applied to domain knowledge. But doesn’t the concept of domain knowledge itself only apply to the production code?

That’s a great question. Tests contain domain knowledge too, but this is the knowledge of a different kind. It’s not about the application itself; it’s the knowledge about how to test that application. There is an overlap between the application domain knowledge and the domain knowledge of the tests, but still, these two sets are not the same:

Both production and test code contain domain knowledge

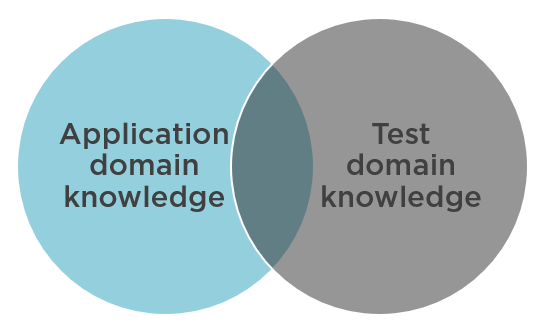
The tests' knowledge lies in the following two things:

The scenarios that need to be performed to verify the application’s correctness
The steps that should be in those scenarios

The scenarios are represented by tests themselves. For example, the division by zero scenario, or the division of two numbers:

[Fact]
public void Division_by_zero()

[Fact]
public void Division_of_two_numbers()

The steps are the content of the arrange, act, and assert sections in those tests. For example, set the divisor and the dividend, check the result, and so on:

int dividend = 10;
int divisor = 2;

response.Result.Should().Be(5);

And so, when you extract common steps from tests, you don’t reuse this knowledge, but remove it from the tests.

You should think of this in terms of what-to's versus how-to's:

The what-to's answer the question of what we are testing. They describe a test scenario using specific steps relevant for that scenario.
The how-to's contain the knowledge of how to implement those specific steps — how these are steps executed.

The DRY principle should be applied to the how-to's, whereas the DAMP principle should be applied to the what-to's.

In other words, you should describe the scenario steps as expressively as possible, but you can (and should) extract any implementation details regarding those steps and reuse them between tests.

Let’s take an example. Let’s say that our calculator API has a memorization functionality and we need to test it. Here’s how this functionality looks:

public class CalculatorController
{
    private int _memorizedDividend;

    public void Memorize(int dividend)
    {
        _memorizedDividend = dividend;
    }

    public Envelope<int> Divide(int divisor)
    {
        if (divisor == 0)
           return Envelope<int>.Error(Errors.DivisionByZero);

        int result = _memorizedDividend / divisor;

        return Envelope<int>.Ok(result);
    }
}

The difference with the initial version is that we can call Memorize() to save the dividend, and then use a Divide() overload that accepts only the divisor.

Here are the tests that verify this functionality:

[Fact]
public void Division_by_zero_with_memorization()
{
    int dividend = 10;
    int divisor = 0;
    var calculator = new CalculatorController();
    calculator.Memorize(dividend); // the additional method call

    Envelope<int> response = calculator.Divide(divisor);

    response.IsError.Should().BeTrue();
    response.ErrorCode.Should().Be("division.by.zero");
}

[Fact]
public void Division_of_two_values_with_memorization()
{
    int dividend = 10;
    int divisor = 2;
    var calculator = new CalculatorController();
    calculator.Memorize(dividend); // the additional method call

    Envelope<int> response = calculator.Divide(divisor);

    response.IsError.Should().BeFalse();
    response.Result.Should().Be(5);
}

Notice the additional method call in both of these tests that brings the calculator into the required state. This method call is part of the overarching step where we setup the calculator.

We can extract the details of how this step is implemented into a helper method:

[Fact]
public void Division_by_zero_with_memorization()
{
    int divisor = 0;
    CalculatorController calculator = CreateCalculatorWithMemorizedDividend(10);

    Envelope<int> response = calculator.Divide(divisor);

    response.IsError.Should().BeTrue();
    response.ErrorCode.Should().Be("division.by.zero");
}

[Fact]
public void Division_of_two_values_with_memorization()
{
    int divisor = 2;
    CalculatorController calculator = CreateCalculatorWithMemorizedDividend(10);

    Envelope<int> response = calculator.Divide(divisor);

    response.IsError.Should().BeFalse();
    response.Result.Should().Be(5);
}

private CalculatorController CreateCalculatorWithMemorizedDividend(int dividend)
{
    var calculator = new CalculatorController();
    calculator.Memorize(dividend);
    return calculator;
}

Note that these tests still contain the setup step itself, we haven’t removed it from the tests. What we did is we abstracted away the details of how this step is performed.

This is the distinction between what-to's and how-to's. The what-to's are still in place: we can clearly see the steps the tests take in order to check the calculation functionality. And we are using descriptive and meaningful phrases when describing these steps — the name of this method communicates its behavior very well. In other words, we are following the DAMP principle here.

At the same time, the details of how this step is performed — the how-to's — are extracted into a single place and reused by tests, thereby following the DRY principle.

This approach combines the best of both worlds:

We don’t need to duplicate the knowledge of how to create the calculator with the memorized dividend.
At the same time, we don’t compromise on the test readability. Thanks to the descriptive name of this method, we don’t need to examine the internals of this step in order to understand the attributes of the created calculator. Because we are keeping all the steps intact, we have the full context of what is going on in the tests.

Moreover, the private method doesn’t couple tests to each other, at least not to the same degree as we had when we extracted the initialization logic into private fields. That’s because tests can still control how they want the calculator be created. They keep that control by passing the required dividend as an argument.

Notice that this rationale is universal and applies to the production code just as much as the test code. In fact, the example with Register and EditPersonalInfo methods also adheres to both DRY and DAMP (I’m copying that example here):

public class UserController
{
    public string Register(string userName, string email)
    {
        if (UserNameAlreadyExists(userName, null))
            return "User with such username already exists";

        if (UserEmailAlreadyExists(email, null))
            return "User with such email already exists";

        // Register the user

        return "OK";
    }

    public string EditPersonalInfo(string userName, string email)
    {
        User currentUser = GetCurrentUser();

        if (UserNameAlreadyExists(userName, currentUser.UserName))
            return "User with such username already exists";

        if (UserEmailAlreadyExists(email, currentUser.Email))
            return "User with such email already exists";

        // Update personal info

        return "OK";
    }

    private bool UserNameAlreadyExists(string name, string currentUserName)
    {
        /* Look in the database if the user name exists */
    }

    private bool UserEmailAlreadyExists(string email, string currentUserEmail)
    {
        /* Look in the database if the user email exists */
    }
}

All steps (what-to's) are intact: we can clearly see that, to register a user, we first need to check if the user name and email already exist in the database. At the same time, the details of how these steps are performed (how-to's), are abstracted away.

Summary

DRY stands for "Don’t Repeat Yourself" and requires that any piece of domain knowledge has a single representation in your code base.
- DRY applies specifically to the domain knowledge, not code lines
DAMP stands for "Descriptive and Meaningful Phrases" and promotes the readability of the code.
People often put these two principles in opposition to each other saying that:
- You can’t apply both DRY and DAMP to the same piece of code
- You should favor DRY over DAMP in the production code, and DAMP over DRY in the test code
The dichotomy between DRY and DAMP is false. Both principles are equally important in both the production and test code.
Think of DAMP and DRY in terms of what-to's versus how-to's:
- What-to's answer the question of what we are doing; they describe the use case (in the case of the production code) or a test scenario (in the case of the test code) using specific steps
- How-to's contain the knowledge of how to implement those specific steps
- The DRY principle should be applied to the how-to's, whereas the DAMP principle should be applied to the what-to's.