C# and F# approaches to illegal state

September 28, 2015

You have probably heard of such phrase as “make illegal states unrepresentable” already. Basically, it stands for using some set of techniques for dealing with illegal states in your domain model. In this post, we’ll look at how C# and F# allow us to handle them.

C#’s approach

Let’s take a User class as an example:

public enum UserStatus
{
    Active,
    Deleted
}

public class User
{
    public string Name { get; private set; }
    public UserStatus Status { get; private set; }
    public DateTime? DeletionDate { get; private set; }
    public List<Subscription> Subscriptions { get; private set; }
}

Here, a user can be either active or deleted. There are two invariants in this example:

While in the deleted state, the user must have the deletion date filled out. The subscription collection should be empty.
A user can have subscriptions only if he/she is in the active state. The deletion date must not be set in this case.

The technique C# traditionally uses to deal with illegal states is called design by contract. If you use the Code Contracts extension, you may specify the invariants explicitly:

[ContractInvariantMethod]
private void Invariants()
{
    Contract.Invariant(
        (Status == UserStatus.Active && DeletionDate == null) ||
        (Status == UserStatus.Deleted && DeletionDate != null && !Subscriptions.Any()));
}

Alternatively, you can use hand-written precondition checks in public methods of the class. Here is how it can be done in C#:

public enum UserStatus
{
    Active,
    Deleted
}

public class User
{
    public string Name { get; private set; }
    public UserStatus Status { get; private set; }
    public DateTime? DeletionDate { get; private set; }
    public List<Subscription> Subscriptions { get; private set; }

    public User(string name)
    {
        Name = name;
        Status = UserStatus.Active;
        Subscriptions = new List<Subscription>();
    }

    public void Delete()
    {
        Contracts.Require(Status == UserStatus.Active);

        Subscriptions.Clear();
        Status = UserStatus.Deleted;
        DeletionDate = DateTime.UtcNow;
    }

    public void Undelete()
    {
        Contracts.Require(Status == UserStatus.Deleted);

        Status = UserStatus.Active;
        DeletionDate = null;
    }

    public void AddSubscription(Subscription subscription)
    {
        Contracts.Require(Status == UserStatus.Active);

        Subscriptions.Add(subscription);
    }
}

As you can see, the User class combines all possible operations and then indicates which of them is applicable to what state. We also manually write code required to satisfy the invariants. For example, when we delete a user, we clear the subscription list, as well as set the deletion date.

We can depict this solution in the following way:

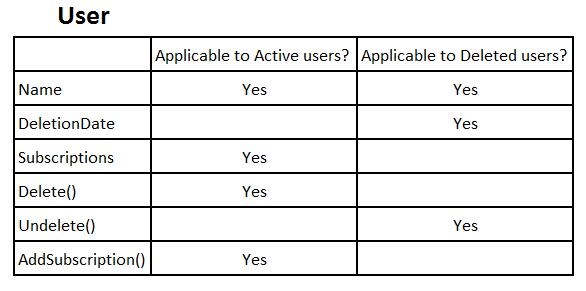C# approach: Cartesian Product of all members and states

The User class is a Cartesian Product of all members and states. The problem here is that some of the combinations are invalid. That is why we use the design by contract approach: it helps us specify in what state the user must reside prior to calling each method.

F#’s approach

F# (as well as other strongly-typed functional languages) traditionally employ a different approach. The bottom line for it is the use of the type system to represent each state separately. This is how the code above can be rewritten in F#:

type ActiveUser =
{
    Name: string;
    Subscriptions: Subscription list
}

type DeletedUser =
{
    Name: string;
    DeletionDate: DateTime;
}

type User =
    | Active of ActiveUser
    | Deleted of DeletedUser

let delete activeUser =
    let { Name = name; Subscriptions = _ } = activeUser
    let deletedUser = { Name = name; DeletionDate = DateTime.UtcNow }
    deletedUser

let undelete deletedUser =
    let { Name = name; DeletionDate = _ } = deletedUser
    let activeUser = { Name = name; Subscriptions = []}
    activeUser

let addSubscription activeUser subscription =
    let { Name = name; Subscriptions = subscriptions } = activeUser
    let activeUser = { Name = name; Subscriptions = subscription :: subscriptions}
    activeUser

Here, we have two separate types - ActiveUser and DeletedUser - which contain only the data that belongs to these user states. Also, the functions now accept either ActiveUser or DeletedUser, but not the User type. For example, the activeUser parameter in the delete function should be of type ActiveUser. If we try to pass it a value of the DeletedUser type, we will get a compilation error.

That gives us a better granularity, so instead of having an all-in-one type, we split it in two:

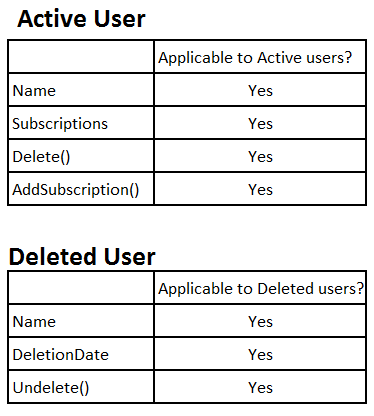F# approach: "normalized" schema F# approach: “normalized” schema

Note that unlike the table for the C# version, this one’s cells are all filled out meaning that we now don’t have any invalid combinations of the states, the data, and the functions.

The differences

The latter solution obviously has a big advantage over the former one. It lifts the invariants into the type system, drastically shortening the feedback loop. With F#, there is no need to run the application in order to validate its correctness. The compiler does all the work for us. The run-time checks we employ in C# using code contracts are simply not required in F#.

We can portray the C#’s approach like this:

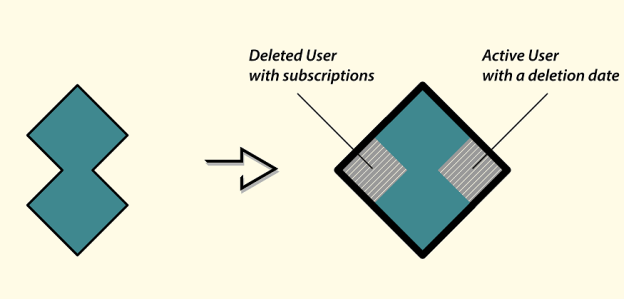C# approach to illegal states

The figure on the left represents the actual shape of the problem we are about to solve. The common way to settle it in C# is to use a coarse-grained solution which, albeit fully covering the problem, brings some redundancy with it. We use the design by contract approach in order to “evict” those redundancies in the run-time.

With F#, on the other hand, we can choose a solution whose shape matches the problem exactly:

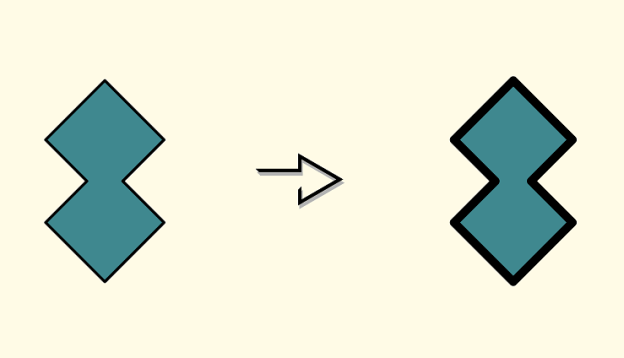F# approach to illegal states

No need to evict the redundancies, because there isn’t any; we exclude the invalid states from our domain model in the first place. That is the reason why we don’t need to use the design by contract approach in F#.

Conclusion

Unfortunately, the lack of discriminated unions and pattern matching makes the F#’s approach mostly unbearable to implement in C#. It’s possible in some simple cases but still remains pretty tedious.

With F#, we are able to make the full use of the power of algebraic types which are extremely helpful for domain modelling.